《妙趣横生的博弈论》7.守门员扑点球的最佳策略是什么

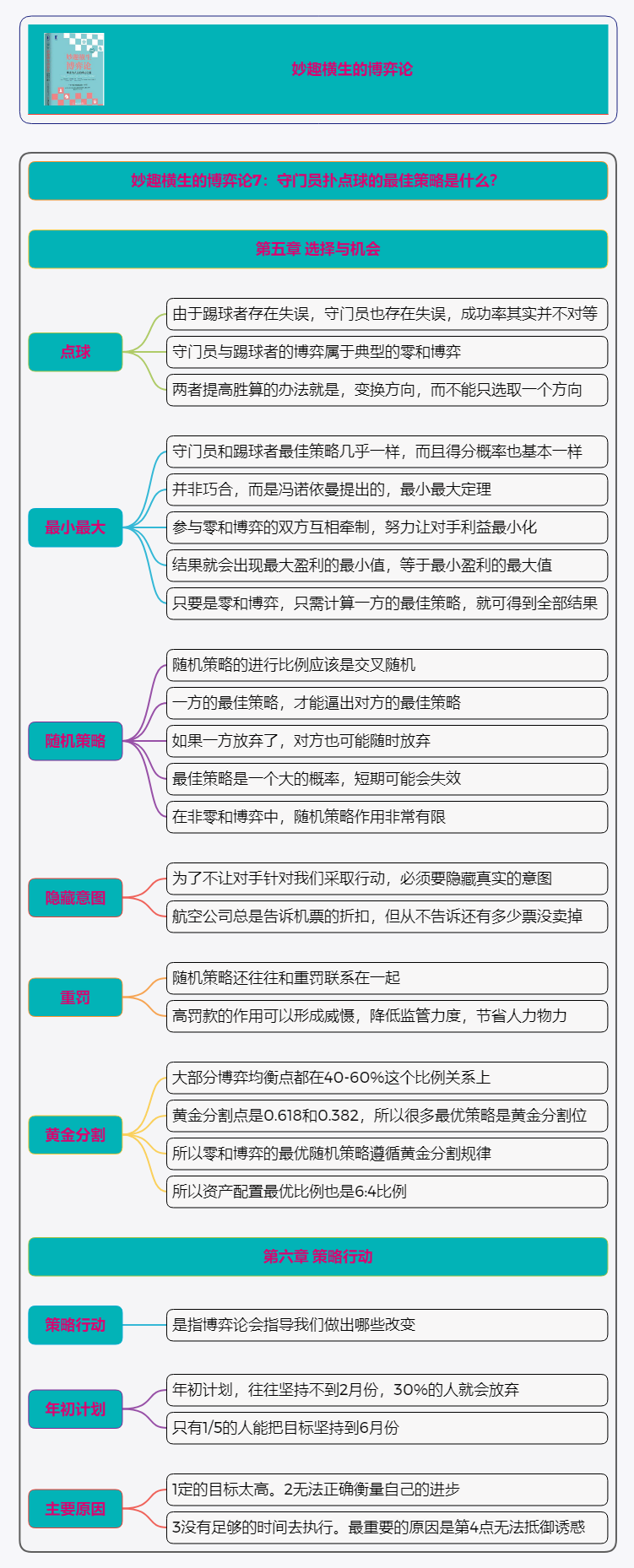
《妙趣横生的博弈论》读书笔记和读后感。昨天你说到了点球问题，守门员得到了踢球者的数据，开启了一场博弈，这场博弈其实就是典型的零和博弈，守门员成功的概率，就等于射门者输掉的概率。有人赢就一定有人输，不存在共赢。

如果是纯策略，也就是踢球者百分百朝着一个方向踢，那么问题很简单，假如守门员猜对了方向，那么我显然射向右路，还有70%的胜算，而射向左路只有58%，那么毫无疑问，我射向右路更划算。

但是70%这个胜算，还是低一些，我如何提高胜算呢，那就要采用混合策略，也就是不能光朝着一个方向踢，还要变换方向，让守门员判断不准。假定守门员一直扑向左边，而你则一半射左侧，一半射向右侧，那么你的混合策略成功率就是50%X58%+50%X93%=75.5%，同理，如果守门员一直扑向右边，那你的成功率就是82.5%，这时候，也就是说，你只要采取各踢一半策略，最低成功率是75.5%，要好于死踢一个方向。那么我们再变换一下，右边把握大，我就用60%的次数踢右侧，左边把握小就踢40%。结果守门员扑向左边的时候，你的成功率就是0.4X58%+0.6X93%=79%，而当守门员扑向右侧，成功率就变成了0.4X95%+0.6X70%=80%，这两个数字也就十分接近了，也就是说，只要你每十次点球，4次左边，6次右边，不管守门员怎么扑救，你都有8成的胜算。这肯定要好于你只踢一边。

那么守门员怎么计算，其实大同小异，计算方法跟上面一样，也是先假设自己各扑向一半的时候，是什么结果，然后再自己的右侧增加次数，可以增加自己的胜算。结果是守门员的最佳策略是左侧比例占41.7%，右侧占58.3%，也是类似一个4:6的策略，这时候踢球者无论怎么射门，守门员成功的概率是在2成左右。

守门员最佳策略和踢球者最佳策略几乎一毛一样，而且得分概率也基本一样，这是巧合吗？并非如此，这就是大科学家冯诺依曼提出的，最小最大定理。也就是参与零和博弈的双方互相牵制，努力让他的对手利益最小化，让自己利益最大化。每当这种博弈出现的时候，就会出现一个令人惊讶的结果，就是最大盈利的最小值，等于最小盈利的最大值。这个结论告诉我们，只要出现零和博弈，我们只需要计算一方的最佳策略，就可以得到全部结果。这其实也是一种纳什均衡，当大家都采取这种策略的时候，对方无论怎么选择，也对结果影响不大。

更复杂的零和博弈就是剪刀石头布的游戏，出一样的不得分，每种手势的概率都是三分之一，这样构成均衡，所以大家的胜率都是一样的。但是全世界竟然有剪刀石头布的世界锦标赛，这么无聊的活动，而且还真有高手在这样的比赛中获益，比如连着出3次布，或者连出3次石头，这些策略，在世界锦标赛中经常使用，据说胜率会提高很多。那些选手认为，并不存在绝对的理论数据，在出招的一刹那，你可以根据身体形态大概判断一个更大的概率。比如现在发点球的时候，守门员也经常用假动作，去诱骗射门者。还有站位以及移动的方式，都会改变均衡结果。

所谓混合策略，并不等于先完成6次向右射门，再完成4次向左射门，他们的进行比例应该是交叉而随机的。从心里学上来说，大家对于随机发生的东西，通常都有一种连续抵触，也就是说，他都出了3次布了，第四次应该不会再出布了。这种情况下，通常会被别人所利用。

另外，当球员得知，守门员拥有最佳策略，无论他选择怎么射门，守门员的成功率都是20%的时候，他是否会变得随意呢？如果他放弃了自己的最佳策略，而是改为只踢一边，那么守门员也很可能会放弃自己的策略。所以这也有相互制衡的问题，你的最佳策略，才能逼出对方的最佳策略，如果你放弃了，对方也可能随时放弃。而且，最佳策略是一个大的概率，并不等于你每踢10次，都有8次会成功，也许你连续8次都被对方扑出去也是有可能的。比如在2000年欧锦赛，意大利的托尔多，就在跟荷兰的比赛中，连续扑出了5个点球。也有曾经的阿根廷射手帕勒莫，一场比赛踢飞了3个点球。所以这种概率长期下来会是这个样子的，但是短期到某一场比赛，还真是说不好什么情况。

在零和博弈中，混合策略可以起到效果，那么在非零和博弈当中呢？混合策略其实作用非常有限，比如商业社会，就并非是零和博弈，作者提到了打折券营销，这是我们常见的商业活动，如果竞争双方都是用打折券，那就无异于价格战，变成了囚徒困境的双输结局，所以都想的是，别人不用而我用，这时候就要抢占先机。比如可口可乐和百事可乐这样的对手，他们就曾经出现过这样的默契，一年52周，而百事和可口分别发放26周的折扣券，绝不同时出现。你说这是一种默契，不如说是蓄谋已久。因为凭借随机的可能性，机会不存在。

还有，为了不让对手针对我们采取行动，我们必须要隐藏真实的意图，比如航空公司总是告诉你机票的折扣，但从不告诉你还有多少票没卖掉，这就是避免有些乘客去根据销量，预测折扣。从而延迟他们的购买行为，最后结果就是大家都不买全价票了，都拖到最后再去抢。现在票价折扣是随机的，你就没办法再去这么做。你也不知道还有多少张，万一卖完了，反而耽误事。

随机策略还往往和重罚联系在一起，比如违章停车罚款200元，有人说太重了，我停车费才10块-20块，你一下罚200，这其实就是一种随机策略，如果罚款跟停车费差不多，那么大家就会心存侥幸，大不了认罚，除非交警足够多，能够每次都抓到违章停车，才能形成威慑，而高罚款的作用，就可以降低监管力度，只需要随机抽查就行，抓到处以10倍停车费重罚。这样就能足以形成威慑。让你乖乖的去交停车费。这就是随机性的妙用。可以节省人力物力，但同时依旧取得很好的效果。类似的还有抓酒后驾车，处罚力度要远大于代驾的费用。因为他本身也是一种随机检查。

二战的时候，还有一个例子，军工厂生产了很多残次品，也就是不能爆炸的炮弹，一开始大家是销毁这些东西，但是后来有人提议，说销毁他还得出人力物力，不如拉到战场上去，随机发射，由于被炮弹打中非死即伤，所以敌人明知道里面有伪劣产品，但也一定不敢放松，必然每颗炮弹都认真拦截，所以其实，利用随机性，就完全可以让这些残次品，发挥正品的效果。远比自己销毁，更加划算。

老齐发现一个规律，不知道大家有没有留意，之前举了很多的例子，最后发现均衡点都在40-60%这个比例关系上，比如之前那个图书馆美女玩色子的游戏，最有策略就是3/8，相当于37.5%，后来踢球这个例子，也是踢球者射向左侧的比例在38.3%，而守门员最佳策略，左侧占比41.7%，这其实遵循一个规律， 就是黄金分割，黄金分割点就是0.618和0.382，所以很多最优策略，都在黄金分割位上。所以当我们发现一个零和博弈，又是一个混合策略的时候，我们应该本能的想到黄金分割。在我们的投资中也是如此，资产配置比例一般也遵循股债6:4或者是4:6的配置，除非特殊情况下，很少上7：3的配置比例，股6债4的配置比例，长期下来，要比股7债3收益还好。是资产配置中，进攻的黄金比例，反过来，防守来说，股4债6，也要比股3债7其实更加稳定。所以我们总说，全配股票未必好，之前有大量数据证实了这一点，但依旧缺乏理论支撑，而这个知识，我们在博弈论中，悟出了答案的理论依据。就是均衡。

下面我们讲策略行动，也就是博弈论会指导我们做出哪些改变，比如有统计显示，我们在年初的时候，通常会定下行动目标，但是往往坚持不到2月份，30%的人就放弃了，只有1/5的人能把目标坚持到6月份，原因主要就是，1大家给自己定的目标太高，2无法正确衡量自己的进步，3没有足够的时间去执行等等，但其实最重要的原因是第4点无法抵御诱惑，比如看到美味牛排的时候，减肥计划就很容易失败，那么我们该如何改善呢？博弈论有没有新奇特的方法。明天我们接着讲。（文章转自老齐的读书圈）