《深奥的简洁》5.地震、物种灭绝与突现

那还能用在哪儿呢？你比如说对于地震的预测。我们今天经常讲里氏多少级地震，这是哪儿来的呢？是一个叫作查尔斯·里克特的人发明的。查尔斯·里克特为了研究地震这件事，他查阅了能够找到的所有地震的资料，他把所有的地震资料找到了以后，把它们分门别类地放在了不同的筐子里边，也就是说他根据里氏规模的这个尺度，把它们分成一堆一堆的。

里氏规模用的是一个对数尺度，什么叫对数？就比如说100，以10为底100的对数就是2，它就是一个幂次对数。他是为了方便我们去对比，每增加一个单位，相对的能量就增加30倍，2级地震比1级地震强30倍，3级地震又比2级地震强30倍，也就是说比1级地震强900倍，那你算一下这个4级地震呢？再乘以30。他找出全世界发生的地震的所有资料，然后把每半级地震分进一个箱子，例如把5~5.5级放进一个箱子，介于5.5~6放入下一个箱子。因为里氏规模本身是对数的，为了在相同的尺度下比较，他们也将这些数字取对数。就是有多少次5~5.5，有多少次5.5~6，多少次6~6.5，把这个数字也取了一个对数。

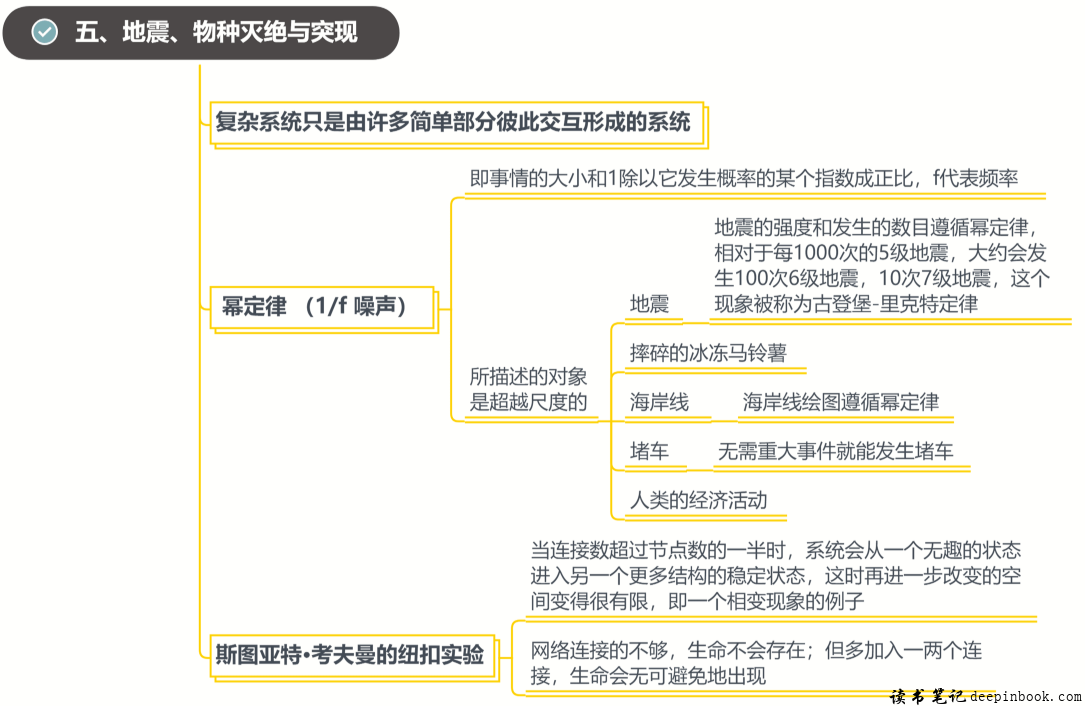
当他们通过画图来显示每个箱子中地震发生的次数的对数和他们的里氏强度的关系的时候，奇迹出现了：这是一条直线，这是一条直线就代表着这里边是有着非常确切的规律的。小地震发生次数非常频繁，大地震很少见，介于两者之间的任何尺度地震发生的次数，都落在两个极端所构成的直线上，这意味着地震的尺度和发生的数目遵循幂定律。

相对于每1000次的五级地震，大约会发生100次6级地震；10次7级地震，这个现象被称为古登堡-里克特定律。这是个第一眼看上去像是个复杂系统，但背后只是简单定律的典型例子。所以人们认为如果一个地方发生过了大地震以后，这个能量得到了释放，那么它就不会再发生更大的地震——其实所有大小地震都是随机发生的，只是频率不同。这一点很重要，也就是说，1906年的洛杉矶大地震发生了以后，第二年再发生一次可能性和100年以后，再发生一次的可能性一样。

就是概率是一样的，并不因为之前发生过后面的概率就变少了。所以在地震带上，任何规模的地震在任何时刻都可能发生，如同丢硬币出现正面的可能性是1/2，尽管先前丢的三次都出现反面。因此在1907年再发生一次像1906年的震级的地震概率，不比在1905年的时候小。

幂定律所描述的对象是超越尺度的，因此任何规模的地震均适用于这个定律。超越尺度就意味着地震震级多大，或者震级多小都符合这条斜线。

那有一个更神奇的实验来了，就是有人为了研究说，宇宙大爆炸的时候，这些星星不是互相碰撞吗？怎么能够模拟出这些碰撞之后，所产生的碎块的分布呢？他们就把马铃薯放在冰箱里边冻硬，把马铃薯冻成完全硬的硬块以后，然后拿着马铃薯照着墙上使劲地摔过去，摔碎。这个摔碎的马铃薯，就形成了大量的大小不一的碎块，然后跟里氏地震的这个分类方法一样，把差不多大小的放一堆，差不多大小的放一堆，然后看这个分布的情况。神奇的现象就是，它同样在对数的数值上是一条斜线，也就是说它们呈现幂次分布。

就是从地震的发生，动物皮毛上的这个颜色，到一块马铃薯冻硬了以后，摔碎的那个块状的分布都是一样。所以这个科学家就讲说，假如你是一个蚁人，或者你是一个小蚂蚁，你小到足够小的这个程度，你走在这个马铃薯块的丛林里边，摔碎了一大堆马铃薯块，然后你从那个当中走，你会和一个人走在地球上的感觉是差不多的。

就是说它周围的那个东西的分布，和我们地球上这些东西的分布，是差不多类似的状态。然后它是用来模拟天上星星碰撞的，那个尺度就是比马铃薯要放大无限倍，依然是符合幂次的定律，是有一个斜率存在的。这个东西有一个非常重要的名词，叫作1/f噪声，什么叫1/f呢？就是比较重大的事件，比如说地震海岸线延展，或者是马铃薯碎片比较罕见，就是比较重大的事件比较罕见，你可以用事件发生概率等于1，除以其尺寸的某个指数来描述这个现象。

换个角度看，你也可以说事件的大小，和1除以它发生概率的某个指数成正比，f代表频率，因为确切的指数其实并不重要，1/f噪声在许多不同系统中自然显现。也就是说一个系统，如果有信息量，如果有规律，它往往就符合1/f噪声的分布状况。幂定律行为和1/f噪声，可以被视为同义词。

这里边最典型的就是宇宙中的，叫作类星体所发出的光，那个东西就是符合1/f噪声的。在一个极端处，也就是1/f相对的是白噪声，它完全随机。就是你将收音机调到没有电台的时候，听到的那个静电干扰杂音，单一频率的噪声是某一音符所发出的纯净但同样无趣的音调；而1/f噪声有时候被称为粉红噪声，听起来才更有意思。

音乐就具有1/f结构，你看这张图这里有一张图，就是描述了古典音乐、摇滚乐、还有人说话的声音。它的频率，就是高音低音不同的频率，出现的次数，跟地震的那个分布的研究方法一样，画了一张图，这个对数图同样是1/f的斜率，也是有这个斜率存在的。

所以为什么人说话声音好听，就人愿意听人声，人愿意听乐器，无论是摇滚乐还是京剧，它都符合1/f频率，它带有信息。但是如果它不带有信息，那就变成了白噪声，或者是单一的一个音调，这个就叫作神秘的1/f噪声。

那你说我们了解了这个东西，有什么好处呢？我们拿它来解释一下都市里边堵车的问题。就是好端端地前面没有发生车祸，为什么会堵车？令人意外的，或者到现在为止也不太意外了，当不同大小的城市被装入箱子，在与相对应的人口数画成对数图的时候，得到的也是一条直线。所以就是说，不论以整个世界或者特定区域来做，结果都一样，人类聚居于城市的行为遵循幂次定律。就是大城市，像北京上海这样的城市几千万人，然后小的地方小到二三十万人，你说为什么呢？为什么这人口分布会差别这么大呢？它是符合1/f噪声的。我只要说符合1/f噪声，就是符合幂次定律的意思。

那么科学家发现堵车也遵循幂定律，我们讨论的堵车模型发生于高速公路，或者没有阻碍的马路上，任何驾驶员都知道，当车子少的时候交通顺畅，一旦车子太多就会堵车。问题在于，如果一辆车因任何原因刹车，他只要跟前面贴得近，他就要刹车，他立刻会使后面的每辆车都慢下来。而且你注意车子减速比加速容易，加速的时候慢，减速的时候快，一脚急刹车砰就刹住了。

20世纪90年代初期，杜伊斯堡大学的研究人员以数学模型在计算机上模拟研究这种行为。在这个模型以及真实交通中，我们都发现了幂定律。不同程度的堵车数，遵循的定律与不同规模的地震数目遵循的定律相同，这明显是1/f噪声运作的例子。

那这里边我们可以学会两个经验，第一个不需要特殊巨大的事件，就能够产生堵车。就是说，我过去就觉得很奇怪，我说北京这是个环路，没有红绿灯，每一个车在那儿走，前面的车跑得快，后面的车跟着，前面那车到出口就出去了，它怎么会堵呢？但是只要刹车，只要前面那车一脚刹车，它可能很快就跑掉了，但这个刹车会往后不断地累积，越往后这些人越慢，最后符合1/f噪声的原理，最后就堵上。所以当你开到前面说什么事，没有任何事，就是堵了。

第二如果车辆密度增高，降低最高限速能够使车流更顺畅。你别忘了它是有数学公式在里边起作用，因为这使得加速与减速之间的时间差别效应减小了。这是真的，如果每个人在拥挤车流中都依照限速行驶，那么他们会更早地到达目的地，就是说那些在车辆车流当中不断穿插，开得特别快，然后造成别人不断地跺刹车的人，实际上是造成了这个交通堵塞的一个非常重要的原因，因为它使得踩刹车的行为变多。实际上如果大家都把速度限到30迈，或者都限到40迈，可能这个大清早起来，四环路上就不会那么堵车了。

这就是对于堵车原理的解释，你会发现我们一会儿讲动物，一会儿讲天体一会儿讲堵车，竟然都是遵循着同一套数学模型，这就是叫作深奥的简洁的原理。那这里边还有什么可以解释呢？人类的经济，经济活动极其复杂，这里边一定有1/f噪声的作用，然后恐龙的灭绝，各种物种的灭绝等等，都是与此相关的。