《深奥的简洁》3.秩序衍生混沌

关于这一点的发现，要说到我们的一个老朋友了，达·芬奇在他那个时候，就曾经发现过这个有趣的状况。达·芬奇在500年前就注意到，一个从石头背后离开往下流的漩涡，并非凭空消失。它先是分解成较小的漩涡，然后每个小涡流又再分解成更小的涡流。在无止境的分流过程中，产生涡流中的涡流中的涡流通向混沌的道路，似乎涉及在无限小尺度下的无限随机作用，至少对乱流的例子是这样。

我们在别处能否找到类似的例子呢？答案当然是肯定的，你们有没有注意过那个肥皂，你洗完了以后上面有很多的泡，而然后你如果仔细去观察那个泡破灭的那个过程，就是一个大泡，嘭，变成几个小泡；几个小泡再变，嘭，变成很多个小泡，然后越来越多的小泡，越来越多的小泡。它就是经过一个相对漫长的时间，一点点破裂一点点破裂，然后大泡变小泡这样慢慢变下去。这个跟这个涡流是一样的一个道理，就是极限循环的吸引子。

在1975年的时候，约克和李天岩，这可能是一个中国籍的科学家，他们发表了一篇文章叫作《周期三蕴含混沌》这个论文，在这个文章当中混沌因此得名。就是从这篇文章开始，1975年，人们开始重视和研究混沌这件事。米切尔·费根鲍姆指出，无论是生物族群的大小、电路的震荡、化学反应的震荡，甚至是经济表现的起伏循环，重点只在于系统必须自我引用，如果符合这个条件，那么系统将会按照同一路径，确实地走向混沌，而不是近似地走向混沌。

这里边重点，别的听不懂不要紧，听到自我引用这件事就知道了。就是混沌系统当中，一定要有自我引用的这个现象。就好像我们说幂次法则，就是为什么一个公司能够做成指数型的公司，因为第一次发展的结果是第二次发展的基础，这是叫自我引用。我迈出一步，我再迈出第二步，假如我迈出的第二步和第一步没关系，那就是线性的活动；但是假如我迈出的第二步一定比第一步大一倍，那就是自我引用。所以一旦产生了自我引用，最终就会走向混沌的这个方向。

同年在1975年分形也被提出来了，提出分形的这个人鼎鼎有名，叫作曼德博。曼德博他说什么叫分形，分形实际上就是碎裂的不规则的石头。我给大家讲讲分形的这个例子，大家就明白什么叫分形了。这里边有一个最简单的分形叫康托尔集合，大家看这幅图，有点像中国《易经》当中的那些爻。就是你把一根线段抹去中间的1/3，那它变成两根线段，把这两根线段又分别抹去中间的1/3，它就变成4根线段，这4根线段再分别抹去中间的1/3，就变成了8根线段。然后每个都抹去中间的1/3，最后它就会变成一系列的点，而它们是完全相似的这种形状，这个就叫作康托尔集合。

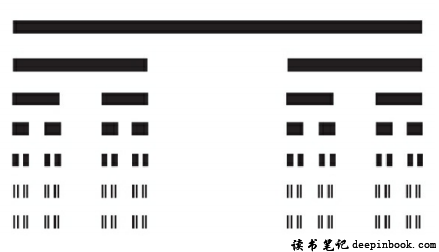
康托尔集合

这是一个最简单的分形，那你说这有什么意思呢？我们来看一个相对复杂一点的，接下来这个叫作谢尔宾斯基三角形，谢尔宾斯基三角形这里边可以有一个很好玩的游戏，大家可以在家里边玩。这是一个黑色的三角形，那么我们在这个黑色三角形当中，倒着再做一个白色的三角形，那就变成了第二个，就抠出来了一个白色的三角形，然后就形成了三个黑色三角形，然后三个黑色三角形当中，都分别抠出一个白色的倒三角形，那就变成了更多的黑色三角形。然后我们在每一个黑色三角形当中——你看自我引用同样的方式——不断地在黑色三角形当中，抠出一个倒的白色三角形，最后所形成的这个缤纷的花纹，这个就叫作谢尔宾斯基三角形。

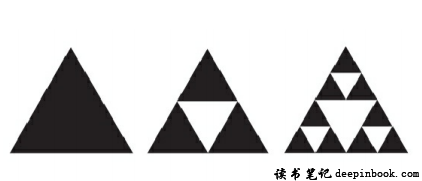
谢尔宾斯基三角形

那你说它的神奇之处在哪儿呢？你回家可以做一个实验，这个实验太神奇了，你用笔拿一支铅笔，然后在本子上画出一个正三角形。画出一个正三角形之后，在这个纸上任意一个地方点一个点，随便一个地方点一个点，然后这个三角形的三个顶点，分别叫123，然后外边的这个点你把它叫作0，这时候你去准备一个骰子，骰子6个面，你把（骰子的）4改成1、5改成2、6改成3，那这样的话这个骰子可以公平地给出，123这三个数字。为什么要用骰子，就是要保证它的随机性。

接下来你就把这个骰子一扔，如果这个骰子出现的是2，那么你就在0点和2点之间的中间选一个点，这个点我们把它叫作4，第四个点了；然后再随便甩一个骰子，这个骰子假如出来的是3，那么你就在这个新的4点和3点之间，中间找一个点，叫作5，然后再骰；骰完以后如果这个又是2，那么就最新的这个5点和2之间的中点，点一个点叫作6；终于骰到1了，那就在6和1之间找一个点7。好了，就是把一个三角形，然后周围不断地找12345这么去选这个点。

你要有足够的耐心，要扔很多下骰子，扔到最后你会发现神奇的现象就是，这些点最终会被吸引到这个谢尔宾斯基三角形当中去，就是它们会构成谢尔宾斯基三角形的这个图案。这里边要注意的就是你要有足够的耐心，而且你得保证它一定是随机的，甚至这个作者说，你都不要去轻易尝试计算机，因为计算机给出的未必是一个真正的随机数，就是用扔骰子的方法就可以看到这个谢尔宾斯基三角形浮现出来。

那你说为什么呢？数学。这就是大自然给我们透露秘密的地方。

那接下来你说这跟自然有什么关系？你没觉得自然当中的很多花纹很多图案很多形状都有规律吗？比如说我们看一下这个分形，就是当我们改变这个分形的公式，改变那个规则，就可以出现完全不同的形状。比如说下面这个叫作羊齿草分形图案，这种图案在森林当中到处可见，就是我们看到很多的树都是长成这样的叶子，这就是一种分形图案，而这种分形图案是用一个公式，然后不断地自我引用不断地迭代做出来，这个就叫作分形。

后来有一个科学家叫科赫，科赫做出了一个科赫曲线。什么叫科赫曲线呢？找一根直直的线，把这个直直的线分成四段，别分开，分成四段，然后挤一下，一个倒的v字就出现了，这是一个倒v字的一个形状。然后你再把这每一个倒v字的，每一个边这不是直的吗，分成四段，再挤一下，慢慢地挤成什么样了呢？就是当你把这个v字型，不断地挤下去的时候，第一步是倒v字型，第二步仿佛出现了一个大卫星，然后第三步就像枫叶，第四步……然后足够多的时候就变成了雪花的样子，这个就叫作科赫图形。

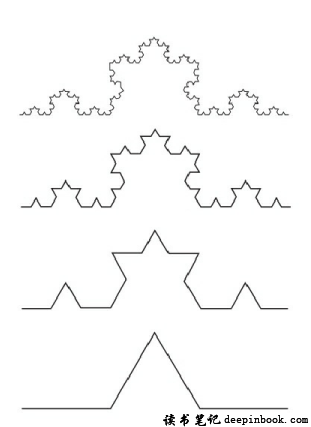
科赫曲线

这个科赫曲线非常重要，因为据说海岸线，人类的海岸线测不准，原因就是海岸线就是这种科赫曲线，它是通过天然的这种演化，然后折叠折叠折叠折叠成现在这个样子，那为什么测不准呢？就在于选取的尺度不一样。假如你以100米为一个单位来测量这个海岸线的话，那你就忽略了中间大量的小于100米的拐弯；那假如你把这个尺度界定成50米，那你就忽略了大量小于50米的拐弯。所以这个数字可以相差极大，就在于你把那个尺度限定到多么细微，这就是科赫曲线所带来的这个影响。

我们的海岸线测不准它的具体的长度，那同样，跟我们的身体也有这样的联系，大家能够想到什么？我们的身体内具备的分形，比如说我们的动脉和静脉，尤其是我们的肾脏上的这个血管。它怎么样能够在我们的体内不占据那么大的空间，但是起到那么大的作用，然后能够分布到全身需要的这种地方？这个是非常神奇的事。也就是说，大自然在创造我们这些物种的时候，它是有数学规律的。这些简单的数学规律，通过自我引用和不断地迭代，最后形成了我们今天这样复杂多样性的完全不同的结果。

那接下来我们就要到了见证奇迹的时刻了，这个有趣的情况都发生在混沌的边缘。也就是说，将进入混沌未进入混沌的那一刻是发生变化的时刻。这里边有一个很著名的例子，就是你看那个沙堆叫沙堆实验，一个沙堆堆在这儿，然后你朝那个沙堆上撒沙子。那一开始这个沙子就不动了，就是一直撒一直撒它一直增长，然后总有那么一刻出现沙崩，出现沙崩的那一刻其实你只扔下去的几粒沙子，但这几粒沙子，跟周围的一些沙子发生了作用，打破了过去的平衡，沙崩，往下走，然后形成了新的平衡，继续再撒又不动了。这个边缘的状态，就是最有趣的值得研究的地方，这就是混沌的边缘。