《微积分的力量》2.第一部分

《微积分的力量》的读书笔记和读后感。首先，我们进入第一部分。在正式解答曲线之谜之前，我们先来简单认识一下，微积分是什么？
说实话，作者在书中给出的答案，和我之前预想的差别有点大。他用一句话就简单说清楚了微积分的核心价值。那就是，让复杂的难题简单化。微积分可以分成两个步骤，切分和重组，也就是说先是把一个复杂的问题分解成无穷个小问题，然后找到这些微小问题的答案后，再把它们重新组合起来。
乍一听，这个策略好像也不难理解，很多善于解决问题的高手都知道，当难题被分解后，就会变得更容易解决。麦肯锡咨询公司曾经提出来的一个MECE原则，说的就是在界定问题时，要把复杂的问题细分成多个可以单独解决的小问题，有了抓手之后当然也方便开展工作。
但是作者在这里提醒我们，微积分真正关键的地方就在于，它把这种，分而治之的策略发挥到了极致，也就是无穷的程度。
它不是把一个大问题切分成有限的几小块，而是无休无止地切分下去，直到这个问题被切分成，无穷多个最微小但是又可以想象出来的样子。这是一个无限做减法的过程，目的就是为了当人们面前有一座珠穆朗玛峰的时候，你能够鼓足勇气迈出最最简单的第一步。
我们把时间拨回到公元前250年左右，当时的古希腊几何学家们，正面对一个特别棘手的问题，他们努力地寻找如何才能迈出第一步的方法。
当时的人们，基本上已经掌握了和直线形状或者是多边形有关的数学方法，比如说如何测量角度，如何利用勾股定理计算边长，或者是计算各种边长与面积的关系。不过，人们对曲线或由曲线形状构成的物体就了解得很少了。比如说圆形，在自然界随处可见，早期的几何学家对圆、球体和圆柱体都很感兴趣，但他们发现，曲线形状分析起来太困难，所有弯曲的东西都难以捉摸。人们无法计算出最基本的圆的面积。
作者提到，微积分的思想就是在这样的背景下诞生了。古希腊数学家阿基米德，利用自己的强大的想象力，提出了一个办法。他的策略是，先把圆想象成一个披萨，然后把这个披萨等分成4块。这4块披萨拆开以后，再把它们上下一块对着一块，像锯齿一样拼合在一起。
你会发现，这个时候，它们看上去有点像一个平行四边形。不过，人们对着这个平行四边形，好像还是无从下手计算出它的面积。但是没关系，只要我们切分的披萨块数足够多，比如8块、16块、32块等，我们得到的图形就会看上去越来越像一个长方形，我把图片贴在文稿中。

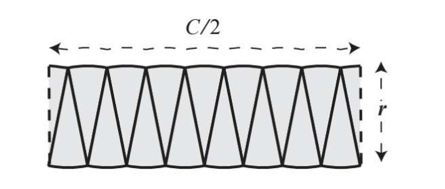
那长方形的面积当然会算，底乘高，得出来的面积也就是圆的面积（1/2 Cr）。
阿基米德的论证过程虽然比我们刚刚说得更加严谨。但是估计你也意识到了，显然，阿基米德通过想象，迈出了第一步。不过紧接着，他又开始好奇，圆的周长C是一条曲线，与圆的直径d，一条直线之间，会不会有什么联系？这就是我们所学的“圆周率π”，π的公式我们当然知道，是C/d。
于是，阿基米德又开始琢磨自己怎样才能计算出圆周率。还是微积分的思想。阿基米德把圆的周长分成很多条微小的直线，虽然我们都知道，圆这么绕一圈，肯定不是由直线构成的，但是在阿基米德看来，只要这些微小的直线数量足够多，那估算也就越准确。
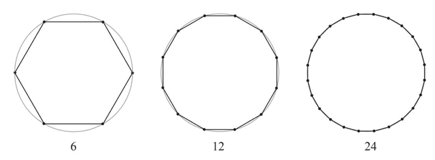
于是，阿基米德选择了从六边形入手，进行一系列计算。之所以选择从六边形入手，是因为六边形包含6个等边三角形，三角形每条边的长度都等于圆的半径r。因此，六边形的周长与圆的直径之比，也就是6r/2r=3，所以，π＞3。当然，六边形看上去还完全不像是一个圆，但对阿基米德来说一切才刚开始。
从六边形中得出结论后，他继续缩短了直线的长度，从六边形到十二边形，再到二十四边形，最终，借助圆内接九十六边形和圆外接九十六边形，阿基米德通过勾股定理，硬生生地算出了π的最终值是：大于3+10/71而小于3+10/70。终于，阿基米德把π限定在了一个具体的范围里，解开了曲线之谜，这在数学史上可以说是一次壮举。

今天的我们当然都知道，圆周率π=3.14159265…，小数点后的数字总是背不完。目前，世界上速度最快的计算机已经算出了圆周率的22万亿个数字，只要算力允许，人们可能会一直算下去。圆周率既没有可见的终点，但又确实存在。它的定义很清晰，就是我们能看见的两个长度，圆的周长和直径之比，但是数本身到底是多少，却又遥不可及。
所以，在作者看来，圆周率正是微积分思想的产物。微积分的思想就是在用无穷来研究有穷，用直线来研究曲线。这是人类发挥想象力实现的一次伟大跳跃。
作者在书中提到，阿基米德建立在微积分思想之上的洞察，比如说利用多边形或者无穷多个部件来进行逼近的方法，直到今天依然熠熠生辉。比如，皮克斯公司的动画师在制作动画的过程中，用到的正是无限切分的方法。动画师通过反复分割一些平面，去逼真地模拟人物布满皱纹的额头、隆起的大鼻子或者是颈部皮肤的褶皱。
我在书里还看到一个有趣的细节，说2009年《阿凡达》电影上映时，为了电影能够更加逼真，潘多拉星球上的每一株植物，动画师都使用了大约100万个多边形来进行模拟，整部影片下来，可以说在当时，《阿凡达》算是第一部使用了数十亿个多边形的电影。
这就是微积分的力量，它帮助人类拿到了第一把破解大自然奥秘的钥匙，一切有关曲线的谜题开始变得有迹可循。